Tree

#  비선형 자료구조의 탐색 방법 : 트리

  자료구조의 가장 핵심적인 내용 중 하나는 탐색이다. 매우 유용한 링크드 리스트의 경우 원하는 자료형에 도달하기 위해서는 하나씩 넘겨가며 찾는 방법 이외에는 없다. 자료가 정렬되어 있다면 이진 탐색이나 보간 탐색 같은 꽤 빠른 탐색 알고리즘을 적용할 수 있지만, 정렬되지 않은 자료들에 대해서는 활용할 수 없다. 

 

이를 보완하기 위한 방법으로 트리를 생각해 볼 수 있다. 트리란 그래프와 유사한 구조이다. 트리를 다른 말로 Connected Acyclic Graph라고도 한다.

 

즉, 모든 노드가 연결되어 있어야 하며 동시에 사이클이 없는 그래프를 트리라고 한다. 

그림1. Cycle 구조

 

  그림1처럼 a-b, b-c, c-a 같이 한 번 지난 노드는 다시 지나지 않을 때 처음 시작 노드로 돌아오는 구조를 Cycle이라고 한다. 트리는 이 Cycle 구조가 없어야 한다.

 

#  트리의 구조

  앞서 설명한대로 트리는 모든 노드가 연결되어 있고 Cycle이 존재하지만 않는다면 만들 수 있으므로, 프로그래머가 필요에 의해 원하는 대로 구성할 수 있다. 때문에 트리의 구성은 정답이 없고, 탐색을 쉽게 할 수 있게 만들어진 대중적으로 많이 배우는 구조들을 간단하게 설명하려 한다.

 

▶ Binary Tree

그림2. Binary Tree

 

  가장 기본적인 트리 구조이다. 아래 ▷ 표시의 트리를 이루는 기본적인 모델이다. 각각의 노드는 왼쪽 자식과 오른쪽 자식을 가리키고 있으며, 이진 트리 자체는 어떤 데이터 저장 규칙이 존재하지 않는다. 저장하는 데이터 형들이 같고 왼쪽부터 차례대로 데이터가 저장된다면, 굳이 구조체를 사용하지 않고 배열만으로 간단하게 구현할 수 있다. 구체적으로 노드를 구성하는 방법은 아래와 같다.

1. 배열의 0번째 자리는 비운다.
2. 최상위 노드 root를 배열의 1자리에 넣는다. 
3. 왼쪽 자식, 오른쪽 자식 노드를 차례로 부모 노드의 배열의 2*n, 2*n+1 위치에 넣는다.

 

 

▷ Heap & Priority Queue

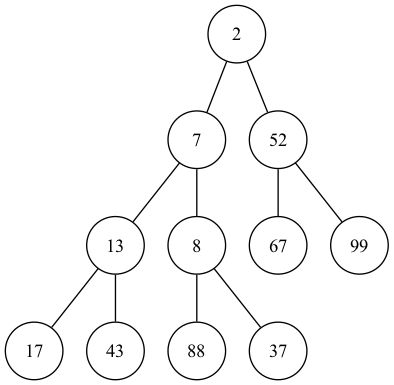
그림3. Heap 구조

 

Heap은 최대 힙, 최소 힙에 따라 루트 노드의 값이 각각 최대값 또는 최솟값으로 구성된다. 이런 힙 구조를 사용해서 정렬 알고리즘을 만든 것이 힙 정렬이고, 힙을 구성하는 규칙이 있기 때문에 노드를 삽입 또는 삭제시에 힙이 재구성된다. 

그림3은 최소 힙을 보여주고 있으며, 힙 규칙이란 부모 노드의 값이 자식 노드의 값보다 적어야 한다.

 

힙을 사용해서 우선순위 큐를 구현한다. 최대 값 또는 최솟 값을 바로 알 수 있기 때문에 구현에 용이하다. 

 

 

▷ Binary Search Tree

 

그림4. BST 구조

 

  이 자료형도 Heap처럼 노드간 규칙을 가지고 있다. 이 규칙이란, 왼쪽 자식 노드의 값 < 부모 노드의 값 < 오른쪽 자식 노드의 값을 만족해야 한다. 이 자료 구조는 특정 값을 탐색하는데 효과적이다. 규칙에 따라 값을 비교하면서 leaf 노드 방향으로 내려가면 된다.  

LeftChild value < Parent value < RightChild value

 

 

※ Binary Search Tree의 문제점

이진 탐색 트리의 문제점은 트리가 편향적으로 자랄 수 있다는 점에 있다.

그림5. 편향된 이진 탐색 트리

그림5는 극단적으로 편향된 이진 탐색 트리를 보여주고 있다. 우리가 트리를 만들게 된 이유는 자료의 탐색에 있는데, 이런 편향된 구조의 트리에서의 탐색은 링크드 리스트에서의 선형 탐색과 다를 바가 없다. 그림5에서 노드 1을 찾으려고 한다면 루트 노드 5에서 순차적으로 내려와야 한다. 자료가 편향된 트리가 나타날 수 있는 빈도가 적다면 이진 탐색 트리를 사용함에 있어 큰 문제가 되지는 않겠지만 실제로는 편향된 트리로 자라는 경우가 많다. 

 

때문에 왼쪽 자식과 오른쪽 자식이 균형을 이루는 트리가 검색에 유리하고, 아래 트리들은 구조를 스스로 바꾸어 균형을 이루도록 구현된다.

 

 

▷ AVL Tree

  이진 탐색 트리의 문제점은 편향된 트리로 자라날 수 있다는 것에 있다. 그럼에도 이 문제점만 해결할 수 있다면 원하는 원소를 O(log n) 시간 안에 찾을 수 있다는 점은 상당히 매력적이다.

  AVL 트리의 모습은 균형이 잘 맞는 이진 탐색 트리와 같다. 다만, Balance Factor라는 인자를 사용해서 노드의 삽입, 삭제 후에 조건에 맞지 않는다면 트리를 회전시켜 트리가 균형을 찾게 만들어준다. 이 BF라는 균형인자의 사용과 트리 구조의 회전은 이 자료 구조의 구현을 어렵게 한다. AVL 트리의 경우 Red Black Tree와 B Tree의 구현이 모두 끝난 후에 구현을 시도해보려 한다.

그림6. AVL Tree

그림6은 원소 1부터 7까지 AVL 트리에 삽입한 모습이다. 최대한 빈 공간을 남기지 않고 원소가 차례로 들어가는 모습을 확인할 수 있다.

AVL 트리 시뮬레이션

AVL Tree Visualzation

트리의 동작 방식을 애니메이션으로 보고 싶다면 위 링크에서 확인할 수 있다.

 

 

▷ Red Black Tree

  AVL 트리와 마찬가지로 몇 가지 복잡한 규칙이 추가된 균형 이진 탐색 트리이다. 이진 탐색 트리와 외관상 다른 점은 트리의 노드에 색이 추가 된 점이다. 레드 블랙 트리도 AVL 트리와 같이 어떤 규칙에 의해 트리가 회전한다. 두 트리 모두 비슷한 기능을 가졌지만, Red Black 트리의 구현이 조금 더 쉽다. AVL의 경우 조건이 레드 블랙에 비해 엄격하므로 오히려 삽입과 삭제 연산이 많은 경우에 오버헤드가 있다. 레드 블랙은 이런 점에서 삽입과 삭제 연산이 많은 경우에 유리하다. 그러나 데이터베이스 검색 같은 정적인 자료를 탐색할 때는 AVL이 빠른 시간을 보장한다.

 

레드 블랙 트리 시뮬레이션

Red/Black Tree Visualization

위 링크에서는 레드 블랙 트리를 직접 그려볼 수 있다. 

 

그림7. Red Black Tree

 

  그림7은 1부터 7까지 원소를 레드 블랙 트리에 삽입한 모습이다. AVL과 같은 순서로 삽입했음에도 모양이 편향된 것 처럼 보인다.

 

 

▶ B-Tree

  우리는 트리의 검색 성능을 향상시키려고 할 때 트리의 계층, 즉 Depth가 많은 영향을 미치는 것을 알 수 있었다. 그렇다면 트리에서의 탐색, 삽입, 삭제 연산의 성능을 향상시키려면 어떻게 해야 할까?

바로 Depth를 줄이면 된다. 지금까지는 자식 노드가 2개인 트리까지만 살펴보았다. 만약 자식 노드가 3개라면 노드가 2개인 트리에 비해 37% 정도 더 빠르다.

 

자식 노드가 2개인 트리 A를 탐색하는 데 걸리는 시간을 $\alpha$, 자식 노드가 3개인 트리 B를 탐색하는 데 걸리는 시간을 $\beta$라 하자.

 

$\alpha = \log_2{n} , \beta = \log_3{n}$ 이다. 

$\frac{\beta}{\alpha} = \log_3{2} \approx 0.631$ 이므로 

$\beta$의 성능은 $\alpha$에 비해 $0.369$배 정도 빠르다. 

 

따라서 노드가 성능이 약 37% 정도 향상된다. 그러나 이는 이상적인 값으로, n이 매우 큰 값이면서 각각의 자식 노드끼리의 값 비교하는 시간을 무시한 결과 값이다.

 

B-Tree는 자식 노드가 M개의 노드를 가질 수 있게 허용한 트리 구조이다.

그림8. B-Tree

B-Tree 시뮬레이션

B-Tree Visualization

 

#  트리와 계층

  앞서 이진 탐색 트리에서 살짝 언급했듯 트리는 계층을 줄이는 것이 탐색에 많은 도움이 된다. 그러나 트리 계층을 줄이는 것이 항상 최선의 결과를 도출하는 것은 아니다. Red Black Tree와 AVL Tree의 경우만 살펴보아도 최적의 Depth를 유지하기 위해 AVL이 적합한 선택이라고 결론을 지을 수 있지만, 자료의 삽입과 삭제가 잦은 데이터를 다루는데는 오히려 트리의 균형 유지 연산에 더 많은 연산이 필요하게 된다. 또한 B-Tree를 사용한다면 Depth를 원하는 만큼 줄일 수 있지만, 반대로 이 경우에는 적절한 곳에 삽입하기 위해 자식 노드끼리 값을 비교해야 하는 경우가 발생하게 된다.

 

  그렇기 때문에 데이터 특성에 따라서 적절한 자료 구조를 사용하는 것이 필요하다. 우리는 자체 구현 OS에서 사용할 파일시스템 구축을 위해 Red Black 트리와 B-Tree를 구현할 것이다. 적절한 구현이 완료된다면 이 글에 블로그 글 링크와 코드를 첨부하겠다.